ഗിയറുകളിലെ സർക്കുലർ പിച്ച് എന്താണ്?

ഗിയർ എഞ്ചിനീയറിംഗിൽ,വൃത്താകൃതിയിലുള്ള പിച്ച്ഒരു ഗിയറിന് ചുറ്റുമുള്ള പല്ലുകളുടെ അകലം വിവരിക്കാൻ ഉപയോഗിക്കുന്ന ഏറ്റവും അടിസ്ഥാനപരമായ അളവുകളിൽ ഒന്നാണ് ഇത്. പവർ ട്രാൻസ്മിഷൻ സിസ്റ്റങ്ങളിൽ ഗിയറുകൾ എങ്ങനെ മെഷ് ചെയ്യുന്നു, ചലനം പ്രക്ഷേപണം ചെയ്യുന്നു, സിൻക്രൊണൈസേഷൻ നിലനിർത്തുന്നു എന്നിവയെ ഇത് നേരിട്ട് ബാധിക്കുന്നു. കൃത്യമായ ഗിയർ രൂപകൽപ്പനയ്ക്കും ഇണചേരൽ ഗിയറുകൾ തമ്മിലുള്ള അനുയോജ്യതയ്ക്കും വൃത്താകൃതിയിലുള്ള പിച്ച് മനസ്സിലാക്കേണ്ടത് അത്യാവശ്യമാണ്.

വൃത്താകൃതിയിലുള്ള പിച്ചിന്റെ നിർവചനം

ഒരു ഗിയർ പല്ലിലെ ഒരു ബിന്ദുവിനും അടുത്ത പല്ലിലെ അനുബന്ധ ബിന്ദുവിനും ഇടയിലുള്ള ദൂരം, പിച്ച് സർക്കിളിലൂടെ അളക്കുന്ന വൃത്താകൃതിയിലുള്ള പിച്ച് (p) ആയി നിർവചിക്കപ്പെടുന്നു.
ദിപിച്ച് സർക്കിൾരണ്ട് ഇണചേരൽ ഗിയറുകൾ തമ്മിലുള്ള സമ്പർക്ക പോയിന്റിനെ പ്രതിനിധീകരിക്കുന്ന ഒരു സാങ്കൽപ്പിക റഫറൻസ് സർക്കിൾ തന്നെയാണ്.

രണ്ട് ഗിയറുകൾ ശരിയായി ബന്ധിപ്പിക്കുന്നതിന്, അവയുടെ വൃത്താകൃതിയിലുള്ള പിച്ചുകൾ തുല്യമായിരിക്കണം, ഒരു ഗിയറിലെ ഓരോ പല്ലും മറ്റൊന്നിലെ പല്ലുകൾക്കിടയിലുള്ള സ്ഥലത്ത് കൃത്യമായി യോജിക്കുന്നുവെന്ന് ഉറപ്പാക്കണം.

ഫോർമുലയും കണക്കുകൂട്ടലും

പിച്ച് സർക്കിളിന്റെ ചുറ്റളവിൽ നിന്നും പല്ലുകളുടെ എണ്ണത്തിൽ നിന്നും വൃത്താകൃതിയിലുള്ള പിച്ച് കണക്കാക്കുന്നതിനുള്ള സൂത്രവാക്യം ഉരുത്തിരിഞ്ഞതാണ്: p=πd​/N

എവിടെ:

•  p = വൃത്താകൃതിയിലുള്ള പിച്ച്

• d = പിച്ച് വ്യാസം (പിച്ച് സർക്കിളിന്റെ വ്യാസം)

• N = പല്ലുകളുടെ എണ്ണം

വൃത്താകൃതിയിലുള്ള പിച്ച് ഗിയറിന്റെ വലുപ്പത്തെയും അതിന് എത്ര പല്ലുകളുണ്ടെന്നതിനെയും ആശ്രയിച്ചിരിക്കുന്നുവെന്ന് ഈ ഫോർമുല കാണിക്കുന്നു - വലിയ ഗിയറുകൾ അല്ലെങ്കിൽ കുറഞ്ഞ പല്ലുകൾ വലിയ പിച്ച് ദൂരത്തിന് കാരണമാകുന്നു.

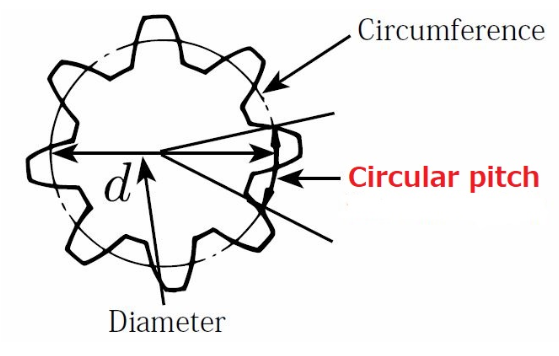
വൃത്താകൃതിയിലുള്ള പിച്ചും ഡയമെട്രൽ പിച്ചും തമ്മിലുള്ള ബന്ധം

സാമ്രാജ്യത്വ സംവിധാനത്തിൽ വ്യാപകമായി ഉപയോഗിക്കുന്ന ഡയമെട്രൽ പിച്ച് (P) എന്നറിയപ്പെടുന്ന മറ്റൊരു സാധാരണ ഗിയർ അളവുമായി വൃത്താകൃതിയിലുള്ള പിച്ച് അടുത്ത ബന്ധപ്പെട്ടിരിക്കുന്നു.

വ്യാസമുള്ള പിച്ച് പിച്ച് വ്യാസത്തിന്റെ ഓരോ ഇഞ്ചിലും ഉള്ള പല്ലുകളുടെ എണ്ണത്തെ പ്രതിനിധീകരിക്കുന്നു, ഇവ രണ്ടും ഗണിതശാസ്ത്രപരമായി ഇനിപ്പറയുന്ന രീതിയിൽ ബന്ധിപ്പിച്ചിരിക്കുന്നു: p=π​/p

ഈ ബന്ധം എഞ്ചിനീയർമാർക്ക് മെട്രിക് അധിഷ്ഠിത (വൃത്താകൃതിയിലുള്ള പിച്ച്) ഗിയർ സിസ്റ്റങ്ങളും സാമ്രാജ്യത്വ അധിഷ്ഠിത (വ്യാസമുള്ള പിച്ച്) ഗിയർ സിസ്റ്റങ്ങളും എളുപ്പത്തിൽ പരിവർത്തനം ചെയ്യാൻ അനുവദിക്കുന്നു.

സർക്കുലർ പിച്ച് എപ്പോൾ ഉപയോഗിക്കണം

പല പൊതുവായ ഗിയർ ആപ്ലിക്കേഷനുകളിലും ഡയമെട്രൽ പിച്ച് സ്റ്റാൻഡേർഡാണെങ്കിലും, ചില പ്രത്യേക സന്ദർഭങ്ങളിൽ വൃത്താകൃതിയിലുള്ള പിച്ച് ഗുണങ്ങൾ നൽകുന്നു:

1. ലീനിയർ മോഷൻ സിസ്റ്റങ്ങൾ (റാക്ക് ആൻഡ് പിനിയൻ):
ഭ്രമണ ചലനം രേഖീയ ചലനമായി പരിവർത്തനം ചെയ്യപ്പെടുന്ന റാക്ക്, പിനിയൻ സിസ്റ്റങ്ങൾക്ക് വൃത്താകൃതിയിലുള്ള പിച്ച് അനുയോജ്യമാണ്. ഓരോ ഭ്രമണവും ഒരു നിശ്ചിത രേഖീയ ദൂരത്തിന് തുല്യമായതിനാൽ വൃത്താകൃതിയിലുള്ള പിച്ച് ഉപയോഗിക്കുന്നത് സൂചികയും സ്ഥാനനിർണ്ണയവും ലളിതമാക്കുന്നു.
2. വലിയ വ്യാസമുള്ള ഗിയറുകൾ:
വലിയ ഗിയറുകൾക്ക്, വൃത്താകൃതിയിലുള്ള പിച്ച് പല്ലിന്റെ അകലം നേരിട്ട് അളക്കുന്നു, ഇത് ഡയമെട്രൽ പിച്ചിനെ അപേക്ഷിച്ച് കൂടുതൽ അവബോധജന്യവും വ്യാഖ്യാനിക്കാൻ എളുപ്പവുമാക്കുന്നു.
3. മെട്രിക് അധിഷ്ഠിത ഡിസൈനുകൾ:
മെട്രിക് എഞ്ചിനീയറിംഗ് സിസ്റ്റങ്ങളിൽ, വൃത്താകൃതിയിലുള്ള പിച്ച് ആണ് തിരഞ്ഞെടുക്കപ്പെട്ട അളവുകോൽ, ഇത് ഗിയർ വലുപ്പത്തിലും കണക്കുകൂട്ടലുകളിലും സ്ഥിരത നൽകുന്നു.

ഗിയർ ജ്യാമിതിയിലെ ഒരു പ്രധാന പാരാമീറ്ററാണ് വൃത്താകൃതിയിലുള്ള പിച്ച്, പല്ലുകൾ എങ്ങനെ അകലത്തിലാണെന്നും രണ്ട് ഗിയറുകൾ എത്ര സുഗമമായി പരസ്പരം ഇഴചേർന്നിരിക്കുന്നുവെന്നും ഇത് നിർണ്ണയിക്കുന്നു. ഈ അളവിന്റെ കൃത്യമായ നിയന്ത്രണം കാര്യക്ഷമമായ ചലന കൈമാറ്റം, കുറഞ്ഞ തേയ്മാനം, മെക്കാനിക്കൽ സിസ്റ്റങ്ങളിലുടനീളം വിശ്വസനീയമായ പ്രകടനം എന്നിവ ഉറപ്പാക്കുന്നു.

ബെലോൺ ഗിയറിൽ, ഒപ്റ്റിമൈസ് ചെയ്ത ടൂത്ത് ജ്യാമിതി ഉപയോഗിച്ച് ഉയർന്ന കൃത്യതയുള്ള ഗിയറുകൾ നിർമ്മിക്കുന്നതിൽ ഞങ്ങൾ വൈദഗ്ദ്ധ്യം നേടിയിട്ടുണ്ട് - ഇത് ആപ്ലിക്കേഷനുകൾക്ക് സ്ഥിരമായ വൃത്താകൃതിയിലുള്ള പിച്ചും കുറ്റമറ്റ മെഷിംഗ് പ്രകടനവും ഉറപ്പാക്കുന്നു.ഓട്ടോമോട്ടീവ്, റോബോട്ടിക്സ്, വ്യാവസായിക യന്ത്രങ്ങൾ.